es学习笔记
1. es入门
2. 各种映射类型1
2.1. 映射分类
-
动态映射:顾名思义,就是自动创建出来的映射。es 根据存入的文档,自动分析出来文档中字段的类型以及存储方式,这种就是动态映射。
-
静态映射:创建索引时指定 mappings
-
具体配置方式
dynamic 属性有三种取值:
true,默认即此。自动添加新字段。
false,忽略新字段。
strict,严格模式,发现新字段会抛出异常。
2.2. 类型推断
| JSON 中的数据 | 自动推断出来的数据类型 |
|---|---|
| null | 没有字段被添加 |
| true/false | boolean |
| 浮点数字 | float |
| 数字 | long |
| JSON 对象 | object |
| 数组 | 数组中的第一个非空值来决定 |
| string | text/keyword/date/double/long 都有可能 |
2.3. 核心类型
2.3.1. 字符串类型
string:这是一个已经过期的字符串类型。在 es5 之前,用这个来描述字符串,现在的话,它已经被 text 和 keyword 替代了。
text:如果一个字段是要被全文检索的,比如说博客内容、新闻内容、产品描述,那么可以使用 text。用了 text 之后,字段内容会被分析,在生成倒排索引之前,字符串会被分词器分成一个个词项。text 类型的字段不用于排序,很少用于聚合。这种字符串也被称为 analyzed 字段。
keyword:这种类型适用于结构化的字段,例如标签、email 地址、手机号码等等,这种类型的字段可以用作过滤、排序、聚合等。这种字符串也称之为 not-analyzed 字段。
2.3.2. 数字类型
| 类型 | 取值范围 |
|---|---|
| long | -2^63到2^63-1 |
| integer | -2^31到2^31-1 |
| short | -2^15到2^15-1 |
| byte | -2^7到2^7-1 |
| double | 64 位的双精度 IEEE754 浮点类型 |
| float | 32 位的双精度 IEEE754 浮点类型 |
| half_float | 16 位的双精度 IEEE754 浮点类型 |
| scaled_float | 缩放类型的浮点类型 |
2.3.3. 日期类型
由于 JSON 中没有日期类型,所以 es 中的日期类型形式就比较多样:
- 2020-11-11 或者 2020-11-11 11:11:11
- 一个从 1970.1.1 零点到现在的一个秒数或者毫秒数。
es 内部将时间转为 UTC,然后将时间按照 millseconds-since-the-epoch 的长整型来存储。
2.3.4. 布尔类型(boolean)
JSON 中的 “true”、“false”、true、false 都可以。
2.3.5. 二进制类型(binary)
二进制接受的是 base64 编码的字符串,默认不存储,也不可搜索。
2.3.6. 范围类型
integer_range
float_range
long_range
double_range
date_range
ip_range
2.4. 复合类型
2.4.1. 数组类型
es 中没有专门的数组类型。默认情况下,任何字段都可以有一个或者多个值。需要注意的是,数组中的元素必须是同一种类型。
添加数组是,数组中的第一个元素决定了整个数组的类型。
2.4.2. 对象类型(object)
由于 JSON 本身具有层级关系,所以文档包含内部对象。内部对象中,还可以再包含内部对象。
PUT product/_doc/2
{
"date":"2020-11-11T11:11:11Z",
"ext_info":{
"address":"China"
}
}
2.4.3. 嵌套类型(nested)
nested 是 object 中的一个特例。
如果使用 object 类型,假如有如下一个文档:
{
"user":[
{
"first":"Zhang",
"last":"san"
},
{
"first":"Li",
"last":"si"
}
]
}
由于 Lucene 没有内部对象的概念,所以 es 会将对象层次扁平化,将一个对象转为字段名和值构成的简单列表。即上面的文档,最终存储形式如下:
{
"user.first":["Zhang","Li"],
"user.last":["san","si"]
}
扁平化之后,用户名之间的关系没了。这样会导致如果搜索 Zhang si 这个人,会搜索到。
此时可以 nested 类型来解决问题,nested 对象类型可以保持数组中每个对象的独立性。nested 类型将数组中的每一饿对象作为独立隐藏文档来索引,这样每一个嵌套对象都可以独立被索引。
{
{
"user.first":"Zhang",
"user.last":"san"
},
{
"user.first":"Li",
"user.last":"si"
}
}
-
优点
文档存储在一起,读取性能高。 -
缺点
更新父或者子文档时需要更新更个文档。
2.5. 地理类型
2.6. 其他类型
3. 搜索相关
routing相关
-
GET操作
- 对于使用了routing写入的文档,在GET时必须指定routing,否则可能导致404
-
查询操作
- 查询操作可以在body中指定_routing参数(可以指定多个)来进行查询。当然不指定_routing也是可以查询出结果的,不过是遍历所有的分片,指定了_routing后,查询仅会对routing对应的一个或一批索引进行检索,从而提高查询效率,这也是很多用户使用routing的主要目的
-
文档的PUT, POST, BULK操作
- 均支持routing参数,在请求中带上routing=xxx即可。使用了routing值即可保证使用相同routing值的文档被分配到一个或一批分片上。
-
UPDATE或DELETE操作
- UPDATE或DELETE操作与GET操作类似,也是先根据routing确定分片,再进行更新或删除操作,因此对于写入使用了routing的文档,必须指定routing,否则会报404响应。
参考:https://cloud.tencent.com/developer/article/1546416
term\match\bool 的区别
https://blog.csdn.net/tanga842428/article/details/75127418
4. es为什么这么快2
Elasticsearch是通过Lucene的倒排索引技术实现比关系型数据库更快的过滤。
特别是它对多条件的过滤支持非常好,比如年龄在18和30之间,性别为女性这样的组合查询。
倒排索引很多地方都有介绍,但是其比关系型数据库的b-tree索引快在哪里?到底为什么快呢?
笼统的来说,b-tree索引是为写入优化的索引结构。当我们不需要支持快速的更新的时候,可以用预先排序等方式换取更小的存储空间,更快的检索速度等好处,其代价就是更新慢。
要进一步深入的化,还是要看一下Lucene的倒排索引是怎么构成的。
4.1. 倒排索引构成

这里有好几个概念。我们来看一个实际的例子,假设有如下的数据:
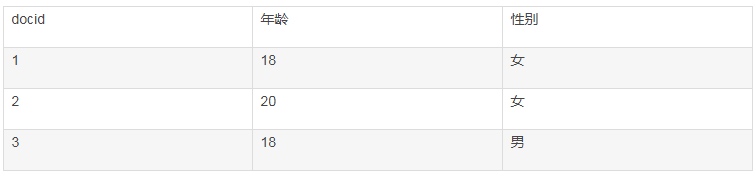
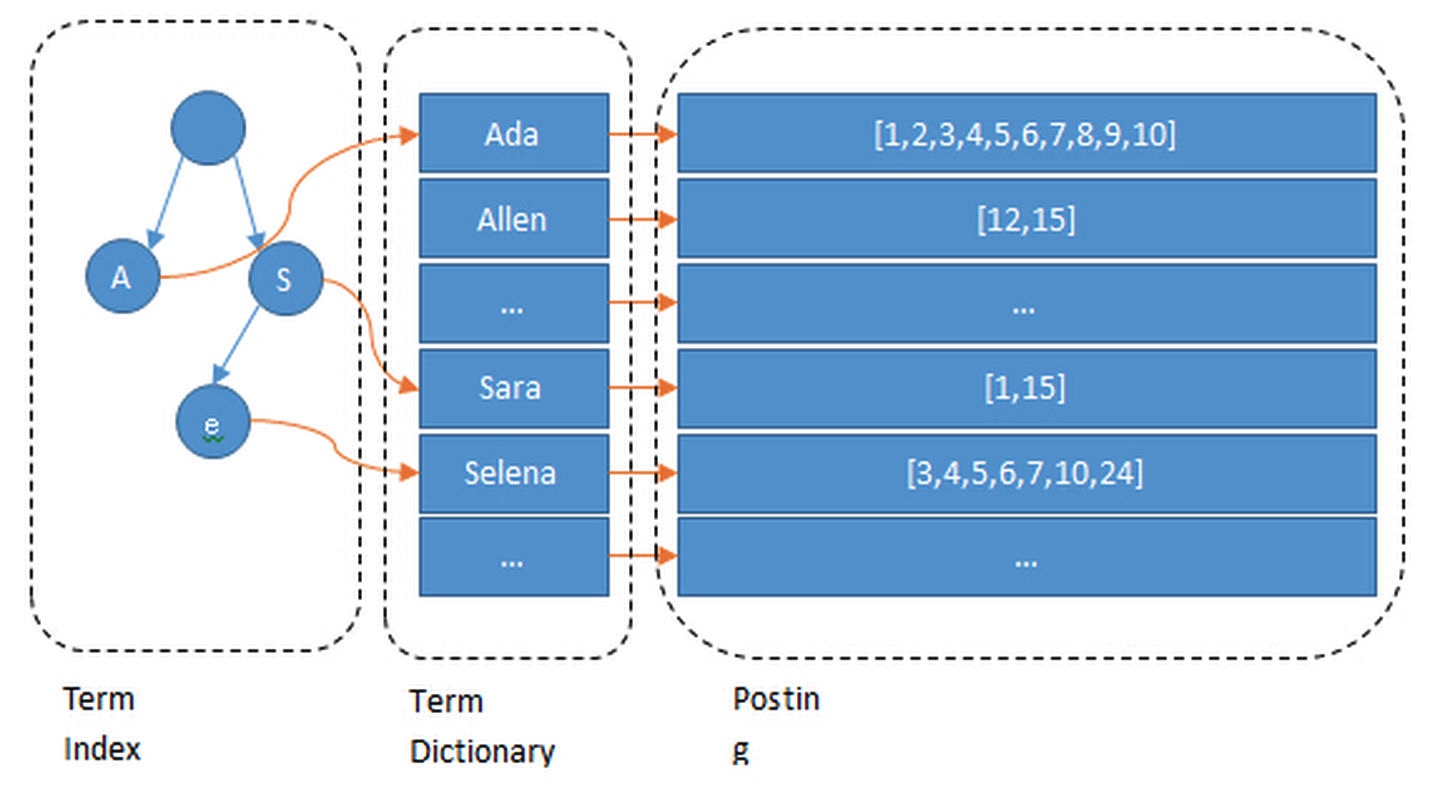
这里每一行是一个document。每个document都有一个docid。那么给这些document建立的倒排索引就是:
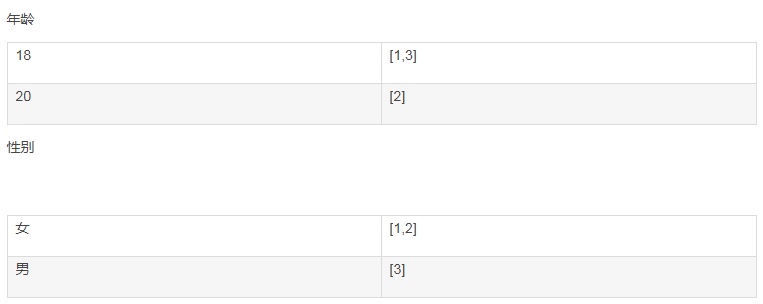
可以看到,倒排索引是per field的,一个字段由一个自己的倒排索引。18,20这些叫做 term,而[1,3]就是posting list。
Posting list就是一个int的数组,存储了所有符合某个term的文档id。
那么什么是term dictionary 和 term index?
假设我们有很多个term,比如:
Carla,Sara,Elin,Ada,Patty,Kate,Selena
如果按照这样的顺序排列,找出某个特定的term一定很慢,因为term没有排序,需要全部过滤一遍才能找出特定的term。排序之后就变成了:
Ada,Carla,Elin,Kate,Patty,Sara,Selena
这样我们可以用二分查找的方式,比全遍历更快地找出目标的term。这个就是 term dictionary。
有了term dictionary之后,可以用 logN 次磁盘查找得到目标。
但是磁盘的随机读操作仍然是非常昂贵的(一次random access大概需要10ms的时间)。
所以尽量少的读磁盘,有必要把一些数据缓存到内存里。
但是整个term dictionary本身又太大了,无法完整地放到内存里。
于是就有了term index。term index有点像一本字典的大的章节表。比如:
A开头的term ……………. Xxx页
C开头的term ……………. Xxx页
E开头的term ……………. Xxx页
如果所有的term都是英文字符的话,可能这个term index就真的是26个英文字符表构成的了。
但是实际的情况是,term未必都是英文字符,term可以是任意的byte数组。
而且26个英文字符也未必是每一个字符都有均等的term,比如x字符开头的term可能一个都没有,而s开头的term又特别多。
实际的term index是一棵trie 树:
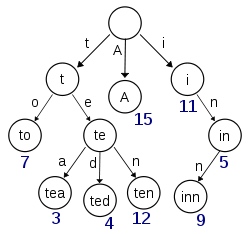
例子是一个包含 "A", "to", "tea", "ted", "ten", "i", "in", 和 "inn" 的 trie 树。这棵树不会包含所有的term,它包含的是term的一些前缀。通过term index可以快速地定位到term dictionary的某个offset,然后从这个位置再往后顺序查找。再加上一些压缩技术(搜索 Lucene Finite State Transducers) term index 的尺寸可以只有所有term的尺寸的几十分之一,使得用内存缓存整个term index变成可能。整体上来说就是这样的效果。
现在我们可以回答“为什么Elasticsearch/Lucene检索可以比mysql快了。
Mysql只有term dictionary这一层,是以b-tree排序的方式存储在磁盘上的。检索一个term需要若干次的random access的磁盘操作。
而Lucene在term dictionary的基础上添加了term index来加速检索,term index以树的形式缓存在内存中。
从term index查到对应的term dictionary的block位置之后,再去磁盘上找term,大大减少了磁盘的random access次数。
额外值得一提的两点是:term index在内存中是以FST(finite state transducers)的形式保存的,其特点是非常节省内存。
Term dictionary在磁盘上是以分block的方式保存的,一个block内部利用公共前缀压缩,比如都是Ab开头的单词就可以把Ab省去。这样term dictionary可以比b-tree更节约磁盘空间。
4.2. 如何联合索引查询?
所以给定查询过滤条件 age=18 的过程就是先从term index找到18在term dictionary的大概位置,然后再从term dictionary里精确地找到18这个term,然后得到一个posting list或者一个指向posting list位置的指针。然后再查询 gender=女 的过程也是类似的。最后得出 age=18 AND gender=女 就是把两个 posting list 做一个“与”的合并。
这个理论上的“与”合并的操作可不容易。对于mysql来说,如果你给age和gender两个字段都建立了索引,查询的时候只会选择其中最selective的来用,然后另外一个条件是在遍历行的过程中在内存中计算之后过滤掉。那么要如何才能联合使用两个索引呢?有两种办法:
- 使用skip list数据结构。同时遍历gender和age的posting list,互相skip;
- 使用bitset数据结构,对gender和age两个filter分别求出bitset,对两个bitset做AN操作。
PostgreSQL 从 8.4 版本开始支持通过bitmap联合使用两个索引,就是利用了bitset数据结构来做到的。当然一些商业的关系型数据库也支持类似的联合索引的功能。Elasticsearch支持以上两种的联合索引方式,如果查询的filter缓存到了内存中(以bitset的形式),那么合并就是两个bitset的AND。如果查询的filter没有缓存,那么就用skip list的方式去遍历两个on disk的posting list。
4.2.1. 利用 Skip List 合并
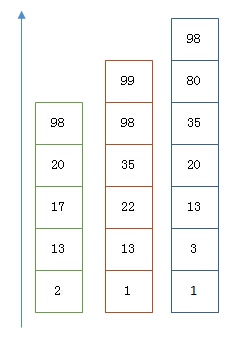
以上是三个posting list。我们现在需要把它们用AND的关系合并,得出posting list的交集。首先选择最短的posting list,然后从小到大遍历。遍历的过程可以跳过一些元素,比如我们遍历到绿色的13的时候,就可以跳过蓝色的3了,因为3比13要小。
整个过程如下
Next -> 2
Advance(2) -> 13
Advance(13) -> 13
Already on 13
Advance(13) -> 13 MATCH!!!
Next -> 17
Advance(17) -> 22
Advance(22) -> 98
Advance(98) -> 98
Advance(98) -> 98 MATCH!!!
最后得出的交集是[13,98],所需的时间比完整遍历三个posting list要快得多。但是前提是每个list需要指出Advance这个操作,快速移动指向的位置。什么样的list可以这样Advance往前做蛙跳?skip list:
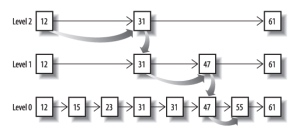
从概念上来说,对于一个很长的posting list,比如:
[1,3,13,101,105,108,255,256,257]
我们可以把这个list分成三个block:
[1,3,13] [101,105,108] [255,256,257]
然后可以构建出skip list的第二层:
[1,101,255]
1,101,255分别指向自己对应的block。这样就可以很快地跨block的移动指向位置了。
Lucene自然会对这个block再次进行压缩。其压缩方式叫做Frame Of Reference编码。示例如下:
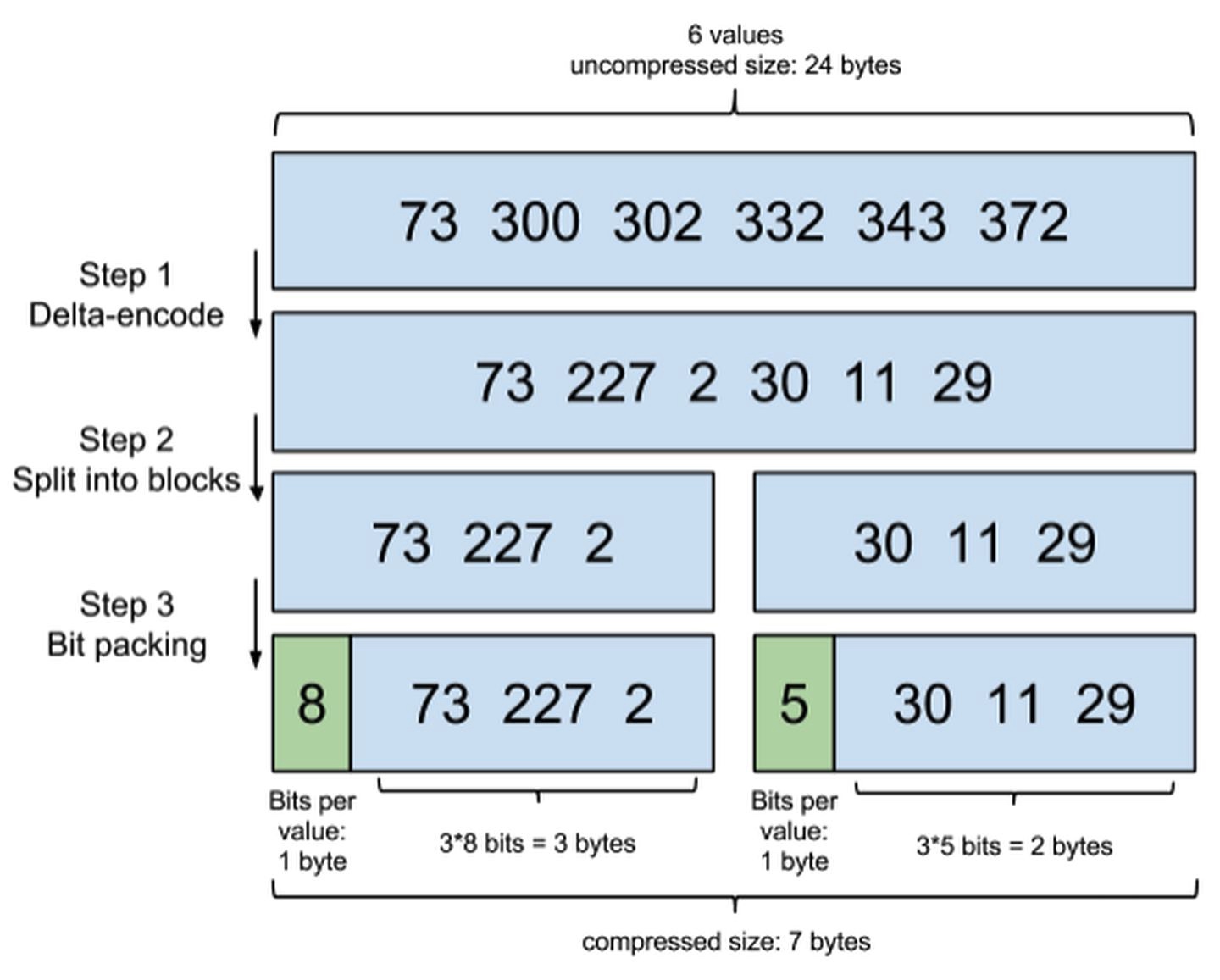
考虑到频繁出现的term(所谓low cardinality的值),比如gender里的男或者女。如果有1百万个文档,那么性别为男的posting list里就会有50万个int值。用Frame of Reference编码进行压缩可以极大减少磁盘占用。这个优化对于减少索引尺寸有非常重要的意义。当然mysql b-tree里也有一个类似的posting list的东西,是未经过这样压缩的。
因为这个Frame of Reference的编码是有解压缩成本的。利用skip list,除了跳过了遍历的成本,也跳过了解压缩这些压缩过的block的过程,从而节省了cpu。
4.2.2. 利用bitset合并
Bitset是一种很直观的数据结构,对应posting list如:
[1,3,4,7,10]
对应的bitset就是:
[1,0,1,1,0,0,1,0,0,1]
每个文档按照文档id排序对应其中的一个bit。Bitset自身就有压缩的特点,其用一个byte就可以代表8个文档。所以100万个文档只需要12.5万个byte。但是考虑到文档可能有数十亿之多,在内存里保存bitset仍然是很奢侈的事情。而且对于个每一个filter都要消耗一个bitset,比如age=18缓存起来的话是一个bitset,18<=age<25是另外一个filter缓存起来也要一个bitset。
所以秘诀就在于需要有一个数据结构:
- 可以很压缩地保存上亿个bit代表对应的文档是否匹配filter;
- 这个压缩的bitset仍然可以很快地进行AND和 OR的逻辑操作。
Lucene使用的这个数据结构叫做 Roaring Bitmap。
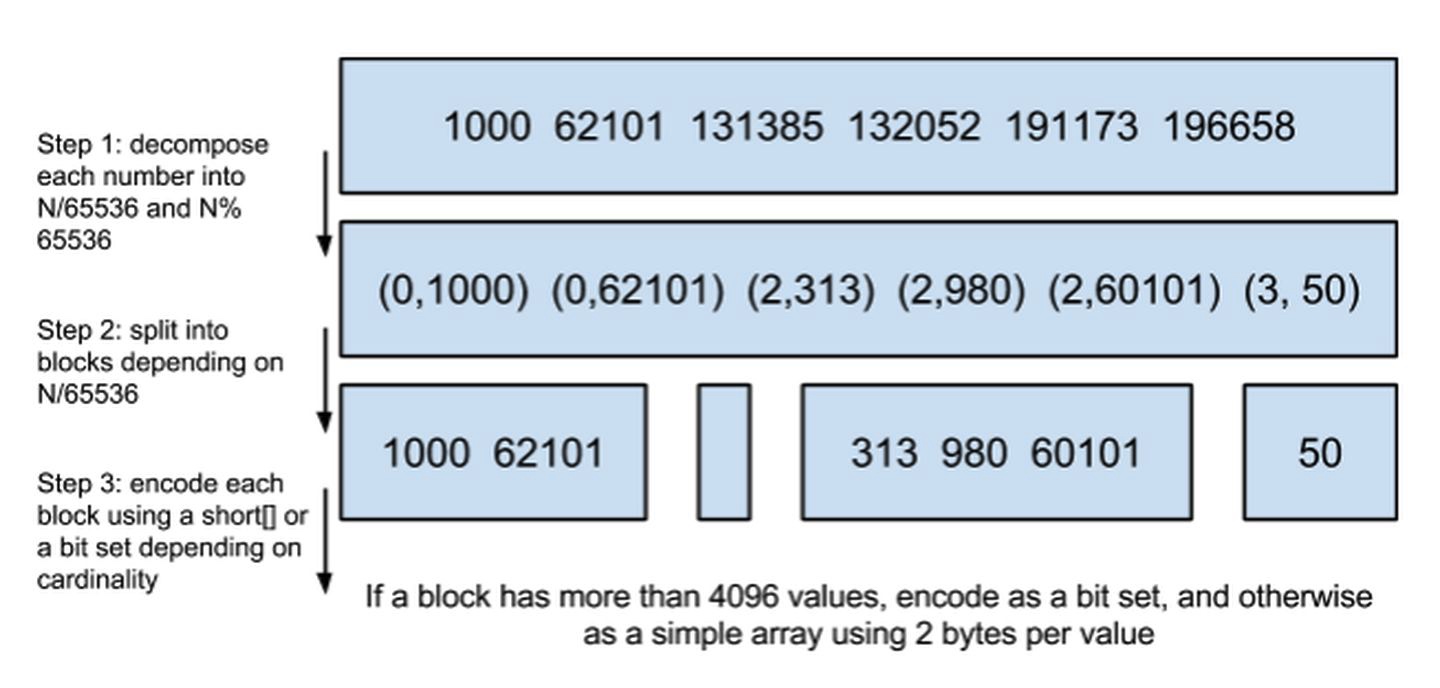
其压缩的思路其实很简单。与其保存100个0,占用100个bit。还不如保存0一次,然后声明这个0重复了100遍。
这两种合并使用索引的方式都有其用途。Elasticsearch对其性能有详细的对比(https://www.elastic.co/blog/frame-of-reference-and-roaring-bitmaps)。简单的结论是:因为Frame of Reference编码是如此 高效,对于简单的相等条件的过滤缓存成纯内存的bitset还不如需要访问磁盘的skip list的方式要快。
4.3. 如何减少文档数?
一种常见的压缩存储时间序列的方式是把多个数据点合并成一行。Opentsdb支持海量数据的一个绝招就是定期把很多行数据合并成一行,这个过程叫compaction。类似的vivdcortext使用mysql存储的时候,也把一分钟的很多数据点合并存储到mysql的一行里以减少行数。
这个过程可以示例如下:

可以看到,行变成了列了。每一列可以代表这一分钟内一秒的数据。
Elasticsearch有一个功能可以实现类似的优化效果,那就是Nested Document。我们可以把一段时间的很多个数据点打包存储到一个父文档里,变成其嵌套的子文档。示例如下:
{timestamp:12:05:01, idc:sz, value1:10,value2:11}
{timestamp:12:05:02, idc:sz, value1:9,value2:9}
{timestamp:12:05:02, idc:sz, value1:18,value:17}
可以打包成:
{
max_timestamp:12:05:02, min_timestamp: 1205:01, idc:sz,
records: [
{timestamp:12:05:01, value1:10,value2:11}
{timestamp:12:05:02, value1:9,value2:9}
{timestamp:12:05:02, value1:18,value:17}
]
}
这样可以把数据点公共的维度字段上移到父文档里,而不用在每个子文档里重复存储,从而减少索引的尺寸。
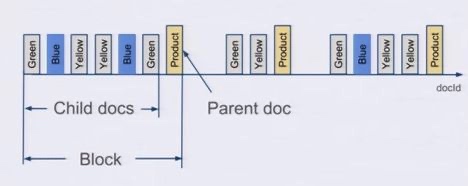
在存储的时候,无论父文档还是子文档,对于Lucene来说都是文档,都会有文档Id。但是对于嵌套文档来说,可以保存起子文档和父文档的文档id是连续的,而且父文档总是最后一个。有这样一个排序性作为保障,那么有一个所有父文档的posting list就可以跟踪所有的父子关系。也可以很容易地在父子文档id之间做转换。把父子关系也理解为一个filter,那么查询时检索的时候不过是又AND了另外一个filter而已。前面我们已经看到了Elasticsearch可以非常高效地处理多filter的情况,充分利用底层的索引。
使用了嵌套文档之后,对于term的posting list只需要保存父文档的doc id就可以了,可以比保存所有的数据点的doc id要少很多。如果我们可以在一个父文档里塞入50个嵌套文档,那么posting list可以变成之前的1/50。
5. es的存储机制是怎样的?3
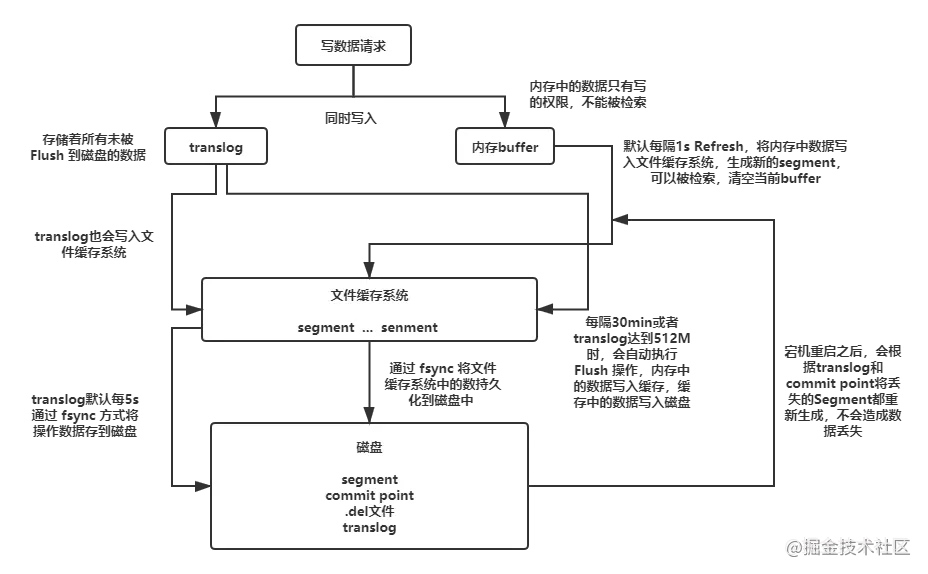
- 一个新文档被索引之后,先被写入到内存中,但是为了防止数据的丢失,会追加一份数据到事务日志中。不断有新的文档被写入到内存,同时也都会记录到事务日志中(日志默认存储到文件缓存系统,每五秒刷新一下到本地磁盘,但是会导致数据丢失,也可以设置参数每个请求都同步,但是性能下降)。这时新数据还不能被检索和查询。
- 当达到默认的刷新时间或内存中的数据达到一定量后,会触发一次
Refresh,将内存中的数据以一个新段形式刷新到文件缓存系统中并清空内存。这时虽然新段未被提交到磁盘,但是可以提供文档的检索功能且不能被修改。 - 随着新文档索引不断被写入,当日志数据大小超过
512M或者时间超过30分钟时,会触发一次Flush。内存中的数据被写入到一个新段同时被写入到文件缓存系统,文件系统缓存中数据通过Fsync刷新到磁盘中,生成提交点,日志文件被删除,创建一个空的新日志。 - 通过这种方式当断电或需要重启时,
ES不仅要根据提交点去加载已经持久化过的段,还需要读取Translog里的记录,把未持久化的数据重新持久化到磁盘上,避免了数据丢失的可能。